Operations and Indexing

Concatenation

You concatenate vectors using the c function; this is the standard way to construct vector objects:

x <- c(1.2, 3.8, NA, 4.4, 1, 2.718)
y <- c(8, 9)
z <- c(x, y)

Recall that there are no scalars in R, so 1.2 is a length-1 vector. The c function creates a new vector by concatenating its arguments together.

Repeating

The rep function constructs a new vector by repeating the elements of its argument.

rep(y, 3)

[1] 8 9 8 9 8 9

rep(y, each = 3)

[1] 8 8 8 9 9 9

The first call repeats the input vector y three times; the second call repeats each element of y three times.

Vector Operations

Most functions in R operate on vectors, and they do so in an element-wise fashion:

log(x)

[1] 0.1823 1.3350     NA 1.4816 0.0000 0.9999

x^2

[1]  1.440 14.440     NA 19.360  1.000  7.388

Binary operators take corresponding elements from their arguments:

a <- c(1, 0, -2, NA, 10)
b <- c(2, NA, 3, 7, 4)
a + b

[1]  3 NA  1 NA 14

a * b

[1]  2 NA -6 NA 40

Note that if either argument is NA, then the result is NA.

Comparison operations result in logical vectors:

a < b  # less than

[1]  TRUE    NA  TRUE    NA FALSE

a == b  # equal to (NOTE double equals)

[1] FALSE    NA FALSE    NA FALSE

a != b  # not equal to

[1] TRUE   NA TRUE   NA TRUE

Other valid comparison operators include <=, >, and >=.

Application: Transforming Variables

Vector operations are useful for transforming variables. For example, in the original bike data, passing distance is slightly skewed to the right:

bikedata <- read.csv("bikedata.csv")
hist(bikedata$passing.distance, col = "firebrick")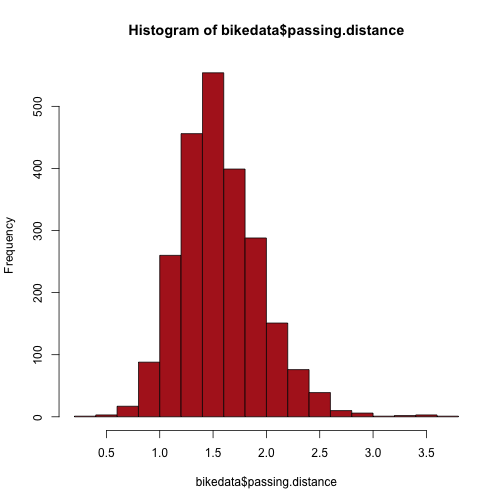

We can adjust for some of this skewness by working with the square root of passing distance:

hist(sqrt(bikedata$passing.distance), col = "steelblue", main = "Square Roots are more symmetric")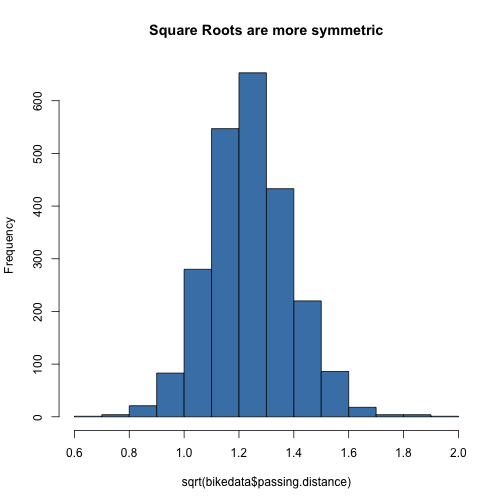

Recycling

When the arguments to a vector function have unequal lengths, the elements of the shorter argument get recycled. This is useful for cases when one argument is a element vector:

10 - x

[1] 8.800 6.200    NA 5.600 9.000 7.282

x/2

[1] 0.600 1.900    NA 2.200 0.500 1.359

Logically, the above two operations are equivalent to rep(10, length(x)) - x and x / rep(2, length(x)).

The recycled vector can have arbitrary length, as in the example

c(1, 2, 3, 4, 5, 6) * c(-1, 1)

[1] -1  2 -3  4 -5  6

Recycling also works in cases where the shorter vector’s length does not divide the longer vector’s, but this is considered bad programming style, and R will issue a warning in such situations.

c(1, 2, 3, 4, 5, 6, 7) * c(-1, 1)

Warning: longer object length is not a multiple of shorter object length

[1] -1  2 -3  4 -5  6 -7

Application: Testing the Empirical Rule

Let’s using recycling and the operations we have learned so far to check if the Empirical Rule holds for the square root of passing distance. First we compute the z scores.

x <- sqrt(bikedata$passing.distance)
z <- (x - mean(x))/sd(x)

Next, we check what proportion have absolute values less than 1, 2, or 3.

mean(abs(z) <= 1)  # Empirical Rule predicts 68%...

[1] 0.6994

mean(abs(z) <= 2)  # ...95%...

[1] 0.9524

mean(abs(z) <= 3)  # ...and 99.7%.

[1] 0.9936

Using the mean function to compute the proportion of TRUE values looks unusual the first time you see it, but this is a common idiom in R. It works by performing the following steps:

Convert TRUE and FALSE values in the input vector to 1 and 0.
Sum the elements of the converted vector. The sum will be equal to the number of TRUE values in the original vector.
Divide by the length of the vector. This will give you the proportion of TRUE values in the original vector.

Integer Indexing

We have already seen slicing (using square brackets). More generally, R supports indexing by any integer vector.

x <- c(-1.1, -1, -3.2, 0.5, 0.9, 0.2, -2.1, 0.1, 0.2, 1)
x[c(3, 1, 7)]  # elements 3, 1, and 7

[1] -3.2 -1.1 -2.1

Negative indices specify omitted elements:

x[c(-3, -1, -7)]  # all elements but 3, 1, and 7

[1] -1.0  0.5  0.9  0.2  0.1  0.2  1.0

You are not allowed to mix positive and negative indices:

x[c(-3, 1, 7)]  # this is an error

Error: only 0's may be mixed with negative subscripts

You are allowed to include 0s in the index set, but doing so has no effect out the output.

You can use integer indexing in a slightly different form to extract particular rows or columns of a data frame.

bikedata[c(2, 4, 6, 19), ]  # rows 2, 4, 6, and 19; all columns

   vehicle colour passing.distance street helmet kerb            datetime
2      HGV    Red            0.998  Urban      N  0.5 2006-05-11 16:30:00
4      Car   <NA>            1.640  Urban      N  0.5 2006-05-11 16:30:00
6      Car   Grey            1.509  Urban      N  0.5 2006-05-11 16:30:00
19     Car   Grey            1.290   Main      Y  1.0 2006-05-12 07:46:00
   bikelane      city
2         N Salisbury
4         N Salisbury
6         N Salisbury
19        N Salisbury

bikedata[c(99, 10, 3), c(2, 4)]  # rows 99, 10, 3, 12; columns 2 and 4

   colour street
99   Grey   Main
10   <NA>   Main
3    Blue  Urban

Application: Top 5 Closest Passes

The next code listing extracts the 5 trips with the shortest passing distances.

shortest <- sort(bikedata$passing.distance, index.return = TRUE)$ix[1:5]
bikedata[shortest, ]

     vehicle colour passing.distance street helmet kerb
988      Car   Blue            0.394   Main      N 0.25
2040     LGV  White            0.493  Urban      N 0.75
1906     Bus  Green            0.510  Urban      Y 0.50
1590     Car  Green            0.527   Main      Y 0.75
1043     Car   Blue            0.636   Main      N 1.25
                datetime bikelane      city
988  2006-05-20 16:21:00        N Salisbury
2040 2006-06-05 15:02:00        N   Bristol
1906 2006-06-05 13:42:00        N   Bristol
1590 2006-05-31 10:14:00        N Salisbury
1043 2006-05-26 15:18:00        N Salisbury

The explanation of the code is as follows:

First, we call sort with index.return=TRUE. This sorts the values returns a list with two components: a double vector named x, which contains the values of bikedata$passing.distance sorted in increasing order, and an integer vector named ix, which contains the indices of these values.
We extract the component of the result names ix with the $ix operator.
Then, we take elements 1:5 and store them in shortest. These are the indices of the 5 smallest values, not the values themselves.
Finally, with the command bikedata[shortest,], we ask for the rows indicated by shortest and all columns of the data frame.

To get the longest passing distance, we can modify the original code, adding decreasing=TRUE to the call to sort:

longest <- sort(bikedata$passing.distance, index.return = TRUE, decreasing = TRUE)$ix[1:5]
bikedata[longest, ]

     vehicle colour passing.distance street helmet kerb
1059     Car   Grey            3.787  Urban      N 1.25
1946     Car  Green            3.571  Urban      N 0.25
992      Car   Blue            3.560   Main      N 0.25
1868     Car  Black            3.489  Urban      N 0.50
1187     Car    Red            3.248   Main      N 1.00
                datetime bikelane      city
1059 2006-05-26 15:18:00        N Salisbury
1946 2006-06-05 14:05:00        N   Bristol
992  2006-05-20 16:21:00        N Salisbury
1868 2006-06-05 12:37:00        N   Bristol
1187 2006-05-27 09:25:00        N Salisbury

If you want the passing distances to be in ascending order, you can use the rev function to reverse the indices:

bikedata[rev(longest), ]

     vehicle colour passing.distance street helmet kerb
1187     Car    Red            3.248   Main      N 1.00
1868     Car  Black            3.489  Urban      N 0.50
992      Car   Blue            3.560   Main      N 0.25
1946     Car  Green            3.571  Urban      N 0.25
1059     Car   Grey            3.787  Urban      N 1.25
                datetime bikelane      city
1187 2006-05-27 09:25:00        N Salisbury
1868 2006-06-05 12:37:00        N   Bristol
992  2006-05-20 16:21:00        N Salisbury
1946 2006-06-05 14:05:00        N   Bristol
1059 2006-05-26 15:18:00        N Salisbury

Logical Indexing

We can use a logical vector to select particular elements of another vector. To do so, the logical vector should have the same length as the original vector. See the following example:

x <- c(0.5, 1.7, -0.8, -1.4, 0.1, -1, -0.4, -0.8, -0.7, 1.7)
y <- c(0, -1.5, -1, -1, -0.1, 0.7, 1.7, -0.2, 0.1, -0.9)
x[x > 0]  # positive values of x

[1] 0.5 1.7 0.1 1.7

y[x > 0]  # corresponding elements of y

[1]  0.0 -1.5 -0.1 -0.9

In the above example, the expression x > 0 evaluates to a logical vector with the same length as x:

x > 10

 [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

When we use this result as an index vector, we get back all of the elements where the index vector is TRUE.

Application: Two-Sample Test

Here is a test of difference in means for the two populations: “square root passing distances without helmet” vs. “square root passing distances with helmet”:

x <- sqrt(bikedata$passing.distance)
h <- bikedata$helmet
t.test(x[h == "N"], x[h == "Y"])


	Welch Two Sample t-test

data:  x[h == "N"] and x[h == "Y"]
t = 5.249, df = 2348, p-value = 1.664e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.02039 0.04471
sample estimates:
mean of x mean of y 
    1.257     1.225

We use logical indexing to extract the sample values drawn from the two populations, then we compare the population means using an unpaired t-test.