Linear Regression

Fit a linear regression model with response variable sqrt(passing.distance) and predictors helmet, vehicle, and kerb. This includes an intercept by default.

bikedata <- read.csv("bikedata.csv")
model <- lm(sqrt(passing.distance) ~ helmet + vehicle + kerb,
            data = bikedata)

Get the coefficient estimates, their standard errors, t statistics, and p values.

summary(model)

Call:
lm(formula = sqrt(passing.distance) ~ helmet + vehicle + kerb, 
    data = bikedata)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.6761 -0.0932 -0.0063  0.0882  0.7455 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.21756    0.02204   55.26  < 2e-16 ***
helmetY     -0.02255    0.00603   -3.74  0.00019 ***
vehicleCar   0.11207    0.02164    5.18  2.4e-07 ***
vehicleHGV   0.04895    0.02674    1.83  0.06726 .  
vehicleLGV   0.09134    0.02299    3.97  7.3e-05 ***
vehiclePTW   0.09773    0.03275    2.98  0.00287 ** 
vehicleSUV   0.11193    0.02456    4.56  5.4e-06 ***
vehicleTaxi  0.06884    0.02977    2.31  0.02083 *  
kerb        -0.10326    0.00850  -12.15  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.145 on 2346 degrees of freedom
Multiple R-squared:  0.0906,	Adjusted R-squared:  0.0875 
F-statistic: 29.2 on 8 and 2346 DF,  p-value: <2e-16

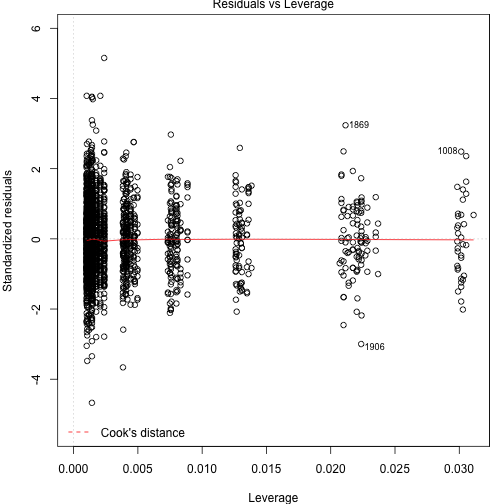
Check regression assumptions with diagnostic plots.

plot(model)

Scatter plot of standardized residuals versus kerb.

plot(bikedata$kerb, rstandard(model))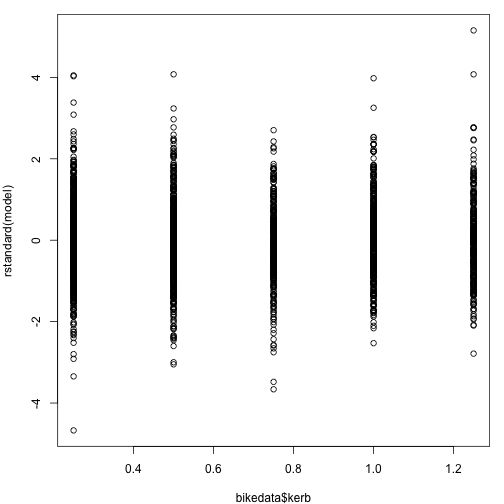

Boxplots of standardized residuals versus helmet

boxplot(rstandard(model) ~ bikedata$helmet)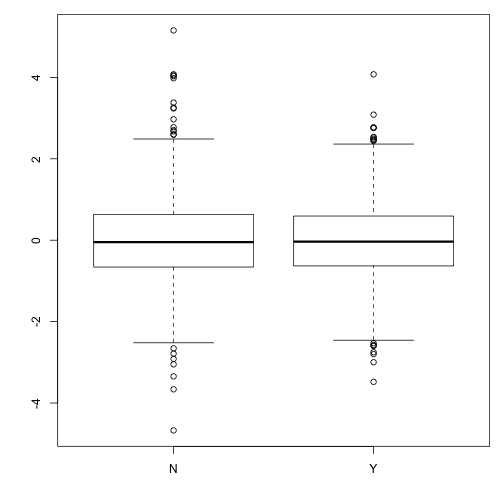

99% confidence interval for coefficient of helmetY.

confint(model, "helmetY", 0.99)

           0.5 %    99.5 %
helmetY -0.03809 -0.007009